
Introduction
If you have read some of my articles or comments, you might remember that I always emphasize that there is no official syllabus for any of the MEXT exams. The Japanese government simply doesn’t offer any information regarding the syllabus. However, many bloggers recommend following the EJU syllabus to understand the MEXT undergraduate math A syllabus.
In a way, I agree with this. Following the EJU syllabus might help, although not as much as practicing the tests. Just because you learn and practice various problems from the syllabus doesn’t fully prepare you for this exam. Therefore, no matter what anybody says, if you truly want to prepare and understand the MEXT undergraduate math A syllabus, then simply do the tests.
All being said, what is this article about? I have analyzed the types of problems for the undergrad math A exam and categorized each problem within a theoretical framework. I did this for 13 years of tests. After that, I centralized the results and did some statistical analysis to see how often certain topics appeared on this test. I also added an evaluation of how long it would take to solve the problems for a regular student and the complexity degree. Here are my findings very briefly.
10 Key Topics in the MEXT undergraduate Math A Syllabus that appeared most frequently
- Inequalities
- Solving quadratic and compound inequalities
- Examples: Solving x^2 – 5x + 6 > 0
- Trigonometry
- Calculating sine and cosine values
- Solving trigonometric equations and identities
- Examples: Finding angles in triangles using sine and cosine rules
- Exponents and Logarithms
- Solving exponential equations
- Simplifying logarithmic expressions
- Examples: Simplifying log_b(a^c)
- Geometry
- Properties of triangles, circles, and inscribed figures
- Calculating areas and lengths
- Examples: Finding the area of a triangle using Heron’s formula
- Sequences and Series
- Working with arithmetic and geometric sequences
- Calculating sums of series
- Examples: Summing an arithmetic series
- Quadratic Functions
- Properties and graphs of parabolas
- Solving quadratic equations
- Examples: Finding the vertex of a parabola
- Probability
- Calculating probabilities with dice, coins, and geometric figures
- Examples: Probability of rolling a sum of 7 with two dice
- Calculus
- Basic integration and differentiation
- Applications to finding areas under curves
- Examples: Integrating f(x) = x^2
- Algebra
- Solving systems of equations
- Polynomial equations and their properties
- Examples: Solving x^2 + y^2 = 1 and x + y = 2 simultaneously
- Statistics
- Mean, variance, and standard deviation calculations
- Examples: Calculating the standard deviation of a data set
Difficulty Assessment and Time Estimation
Based on past exams (2007-2020), the tests have maintained a balanced difficulty level with a mix of moderate and challenging questions. Here’s a summary of the average estimated time required for various question types:
- Moderate Questions: Approximately 10-15 minutes per question
- Challenging Questions: Approximately 15-20 minutes per question
Observations and Trends
- Increasing Complexity: Over the years, the exams have introduced more complex problems, particularly in calculus and trigonometry.
- Time Management: Despite the increasing difficulty, the allocated time remains 60 minutes, requiring efficient time management from students.
- Variety of Topics: A consistent inclusion of core topics such as algebra, geometry, trigonometry, and calculus with a slight increase in problem diversity.
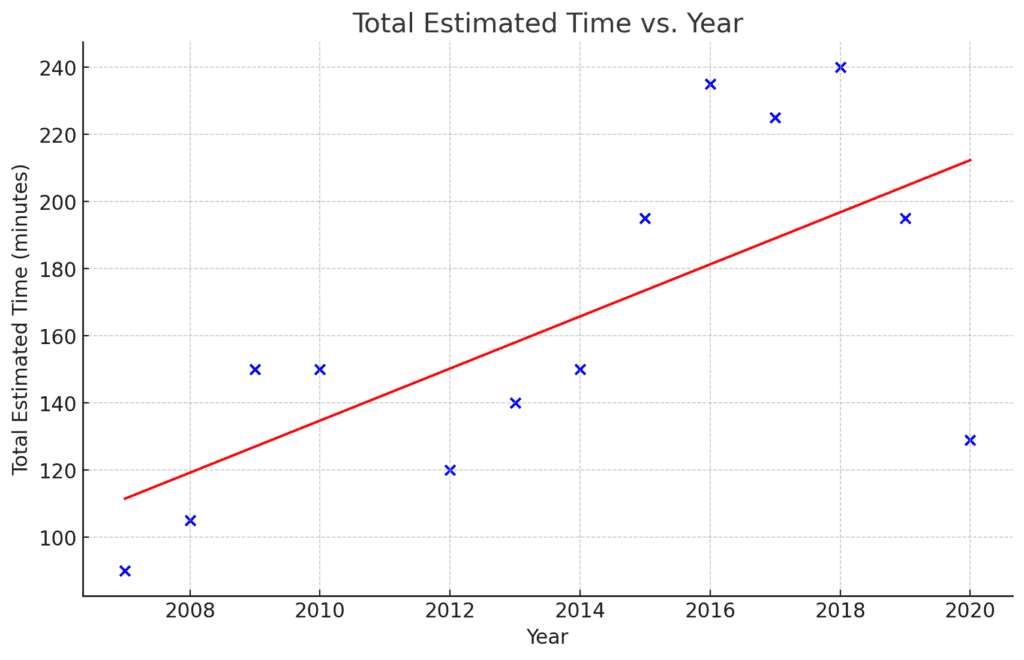
Navigating the Increasing Complexity of MEXT Math A Exam
Keep in mind that although the tests have mixed questions, some easier and some more difficult, the trend is to become increasingly difficult. This is because of the time constraint (one hour per test) and the complexity of the problems.
I had difficulties solving some concepts presented in the MEXT undergraduate A exam because I had never studied them. This is because I first had to study the concepts myself and then explain them in my books. Examples include vectors, which I studied very briefly during high school, solids and calculating volumes starting with their equations, elongating solids and calculating the new volume, etc.
Now, I think these are easy. However, at first, I could not differentiate between the equation of a cone and a cylinder. Honestly, I talked with too many students who have trouble understanding and solving systems of equations, systems of inequalities, and absolute value, not to mention more advanced concepts such as equations of solids.
Practical advice that you can actually apply in the real world
1. There are no shortcuts. Do the work, and you will be rewarded.
Someone recently wrote to me saying they took a week off to prepare for this exam. This is not an isolated case.
I don’t want to be pessimistic or discourage students, especially if they are already in this situation. Still, you cannot expect to pass this without learning. The result will be reflected by the effort you’ve put into preparing for it. This is why I usually recommend about two years of preparation before applying for the MEXT scholarship.
2. Practice the past tests.
Simply working from different books or from the Internet is not enough. It is good, but it should be an addition to your main preparation, not the other way around.
Practice past tests, get the feel of the exam, and become familiar with the format and concepts. Then, for each problem, find other similar problems or more complex concepts to practice. The tests should be number one, followed by additional materials based on the tests, and then additional materials based on the EJU syllabus.
3. Time management and focus
If you wonder if anybody could actually solve the MEXT exam within the 60-minute limit, the answer is yes. I have heard from students who solved everything, and some very quickly, as in 30 minutes. So, it is possible. This is the level of competition you are getting yourself into.
You need to practice a lot to achieve this, especially under time restraints. When you see the test, you must be so focused that you start solving it quickly. You don’t have time for trials and errors.
Your Journey Ahead (Conclusion)
Remember your goals and dreams, which are to go to Japan, to experience life as a MEXT student, to develop and evolve, to become more and to expand your limits. Nothing can keep you from achieving these except yourself and your beliefs. Believe it, and you are halfway there. Prepare for it, and it will be yours. Do not be in a hurry; take your time to reflect.
I intend to do a similar analysis of the syllabus for MEXT undergraduate math B, Special Training College, and College of Technology, so please leave a comment below with your thoughts on what I should introduce or if you believe something’s missing. I always love hearing from you all! Best of luck in achieving your dreams!



